interference - difrakce

OPTICKÁ DRÁHA (2nd) JE VZDÁLENOST, KTEROU SVĚTLO URAZÍ VE VAKUU ZA STEJNÝ ČAS JAKO V DANÉM LÁTKOVÉM PROSTŘEDÍ.


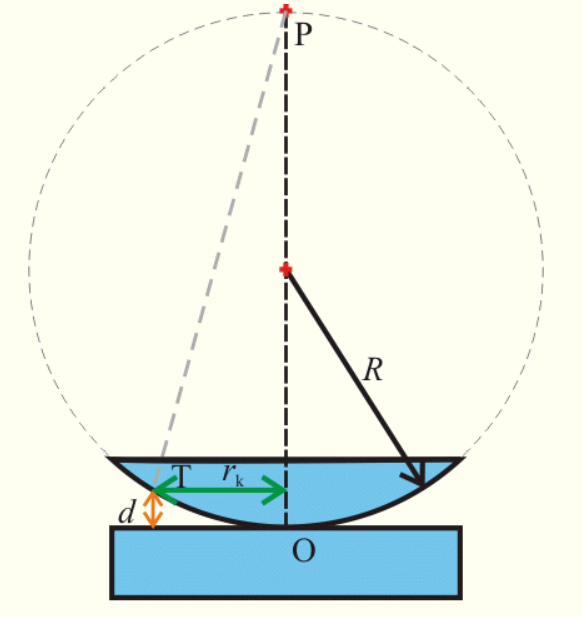
Newtonova skla jsou jednoduchá zařízení, kterými lze pozorovat interferenci. Jsou tvořena skleněnou deskou (tzv. planparalelní deska), k níž je přiložena ploskovypuklá čočka (tj. čočka, jejíž jedna plocha je rovinná, druhá kulová), viz obrázek. Kulová plocha čočky má velký poloměr křivosti, který označíme R. V okolí místa dotyku čočky s deskou vzniká tenká vzduchová vrstvička o tloušťce d, jež se mění se vzdáleností od středu čočky. Interferenční obrazec pro monofrekvenční světlo dává střídající se světlé a tmavé kroužky, kterým se říká Newtonovy kroužky. Při použití bílého světla vznikají Newtonovy kroužky duhových barev.
Na obrázku je schématický nákres, kde R je poloměr křivosti kulové části čočky, d je tloušťka vzduchové vrstvy, rk je poloměr interferenčního kroužku, kde k je pořadové číslo kroužku - např. řád maxima. Písmena T, O, P jsou body na kružnici o poloměru R.
Příklad:
Aby se na skleněných čočkách zabránilo zpětným odrazům světla, bývají pokryty tenkými vrstvičkami materiálu, který má index lomu nižší než podkladová vrstva. Jejich tloušťky se volí tak, aby se paprsky světla zvolené vlnové délky po odrazu na přední a zadní straně rozhraní vrstvičky (zpět ke zdroji světla) interferencí vzájemné vyrušily. Jaká minimální tloušťka vrstvičky fluoridu hořečnatého zajistí, aby na ní nedocházelo ke zpětnému odrazu světla v oblasti okolo 550 nm, ve které je lidský zrak nejcitlivější? Index lomu skla je 1,52, vrstvičky 1,38.
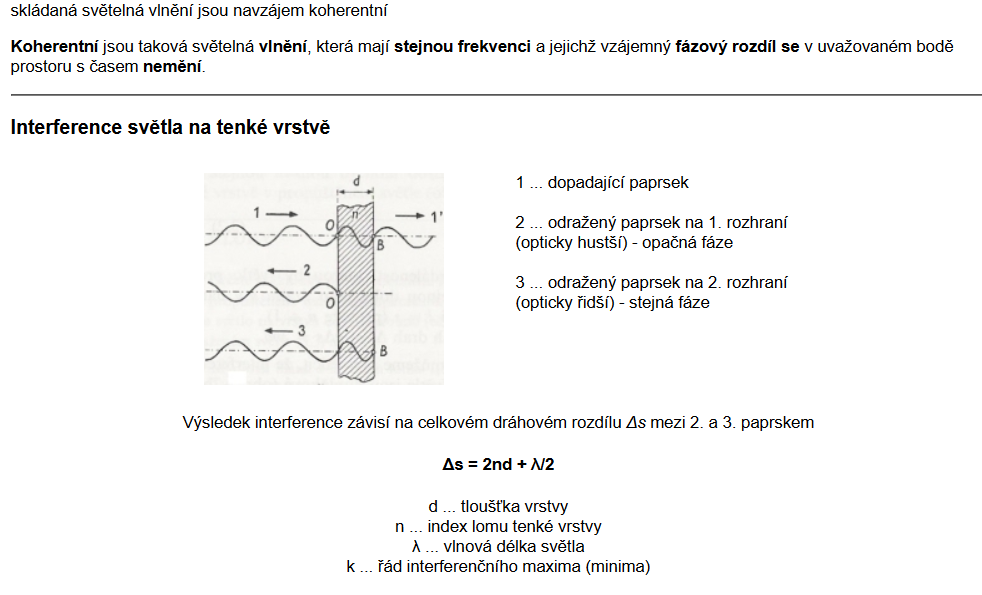
- Jak probíhá interference na tenké vrstvě?
- Jaké paprsky se spolu budou skládat a jaký bude celkový dráhový rozdíl těchto paprsků?
Na obrázku je černý paprsek přicházející od zdroje. Když dorazí na první rozhraní, částečně projde dál, částečně se odrazí a přitom změní fázi, což nám naznačuje modrý (odražený) paprsek na druhém obrázku. Když dojde černý paprsek na druhé rozhraní, také se částečně odrazí, a opět svoji fázi změní, to nám ukazuje červený paprsek na třetím obrázku. V obou případech totiž dochází k odrazu na opticky hustším prostředí, tedy i ke změně fáze. Bude nás zajímat, jak se spolu složí červený a modrý paprsek.

Jak vidíme na obrázku, oba paprsky se odráží s opačnou fází. Tyto změny se navzájem vyruší a nebudeme s nimi počítat. Jediný dráhový rozdíl, který je pro nás důležitý, je dráha, kterou musel druhý (červený) odražený paprsek urazit navíc. Tedy:
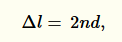
kde n je index lomu antireflexní vrstvy a d je tloušťka antireflexní vrstvy.
Jelikož nás zajímá, kdy se paprsky zeslabí, potřebujeme znát vztah pro interferenční minimum. To nastává, když se dva paprsky potkají dráhovým rozdílem rovným lichému násobku poloviny vlnové délky:
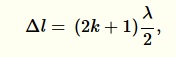
protože chceme nejtenčí vrstvu, dosadíme za k = 0.
Tloušťka antireflexní vrstvy, která pokrývá čočku, je přibližně 100 nm.
Někdy potřebujeme, aby odrazivost materiálu byla malá, v jiných případech je lepší velká. U fotoaparátu je výhodné odrazivost snižovat, aby většina světla prošla čočkami fotoaparátu a fotka byla správně osvětlená. Někdy se však snažíme odrazivost zvýšit. Například na bižuterii se nanáší materiály s větším indexem lomu, aby se určité vlnové délky zesílily a šperky získaly barevné odlesky.
V předchozím řešení jsme nebrali v úvahu odraz obou paprsků s opačnou fází. Řekli jsme, že se vyruší a tedy není nutné s nimi počítat.
Teď ovšem s nimi počítat budeme. Napíšeme si dráhové rozdíly obou paprsků do detailu: první paprsek se odrazí s opačnou fází:
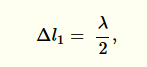
druhý paprsek se odrazí s opačnou fází a k tomu projde navíc optickou dráhu 2nd:
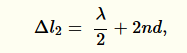
takže dráhový rozdíl obou paprsků bude:
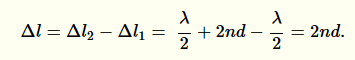
Příklad:
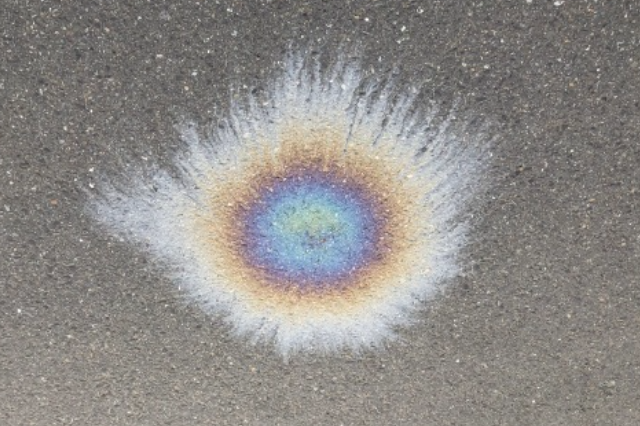
Na skvrnu oleje tloušťky 200 nm vytvořené na vodě dopadá kolmo sluneční světlo. Určete vlnovou délku světla, která se bude po odrazu nejvíce zesilovat. Tato vlnová délka nám určí, jak barevná se nám bude skvrna zdát při pohledu shora.
Když světlo dopadne na olej, částečně se odrazí a částečně projde.
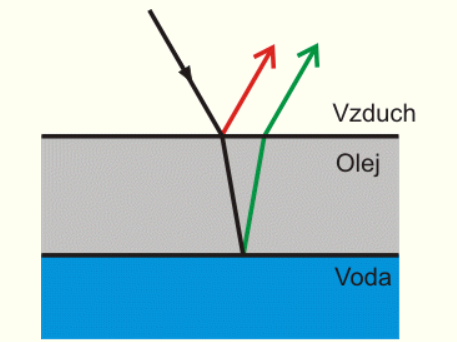
Pro názornost je obrázek namalován pro šikmo dopadající paprsky, ale úlohu řešíme pro kolmo dopadající paprsky.
Černý paprsek přichází od zdroje a na prvním rozhraní se část odrazí - tato část je značena jako červený paprsek. Pokračující část paprsku projde olejem a odrazí se na druhém rozhraní - zelený paprsek.
O kolik jsou vzájemně fázově posunuty červený a zelený paprsek?
Jak ovlivní fázi vlny její odraz? Jak se tato změna projeví na dráhovém rozdílu?
K odrazu dochází vždy na rozhraní dvou optických prostředí. Jako opticky hustší označujeme to prostředí, které má větší index lomu, a je zde tedy menší rychlost šíření světla.
Rozebereme dva případy, kdy světlo dopadá:
2) z opticky hustšího prostředí na prostředí opticky řidší.
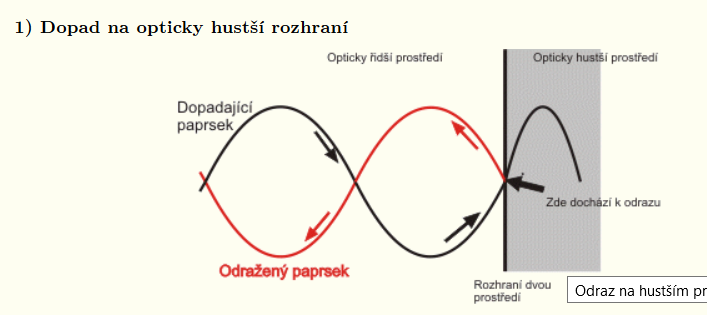
Černý paprsek dojde od zdroje k rozhraní mezi prostředími. Zde dochází k odrazu na opticky hustším prostředí, a proto zde dojde k odrazu s opačnou fází. Změně fáze na opačnou odpovídá dráhový rozdíl Δl = λ/2.
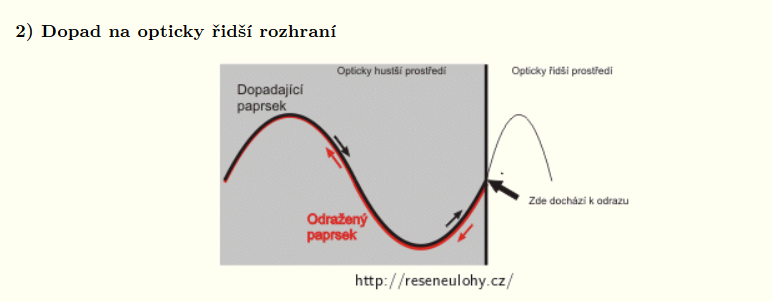
Černý paprsek dojde od zdroje k rozhraní mezi prostředími. Zde dochází k odrazu na řidším prostředí, a proto dojde k odrazu se stejnou fází. Tomu odpovídá nulový dráhový rozdíl, tj. Δl = 0.
Tyto děje mají analogii v mechanickém vlnění. Pokud vezmeme provaz, upevníme ho např. ke stěně a zkusíme vyslat vlnu, pevný konec lana způsobí odraz s opačnou fází stejně jako ve výše uvedeném prvním případě. Pokud ovšem necháme lano volně, dojde na jeho konci k odrazu se stejnou fází.
Jak se v dráhovém rozdílu projeví skutečnost, že v oleji se světlo šíří pomaleji?
Pokud máme vlnu, která prochází přes prostředí s jinými indexy lomu, dochází zde ke změně vlnové délky.
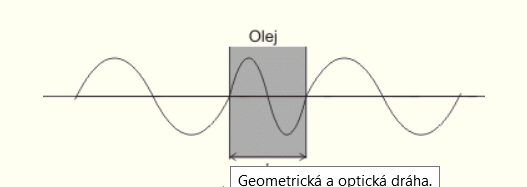
Geometrická dráha paprsku je stejná jako tloušťka prostředí d. Pro interferenci je ale podstatné, s jakou fází se paprsky potkají, což ovlivňuje nejenom geometrická vzdálenost, kterou urazily, ale i rychlost šíření světla, tj. index lomu prostředí. Chceme zjistit, jakou vzdálenost by světlo urazilo, pokud by místo látkou (zde olejem) letělo vakuem. Protože index lomu n znamená, kolikrát je světlo v daném prostředí pomalejší než ve vakuu, je hledaná vzdálenost, tzv. optická dráha l rovna:
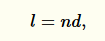
kde n index lomu prostředí a d je skutečně uražená vzdálenost.
Jaký bude celkový dráhový rozdíl obou paprsků?
Nakreslíme si, jak bude vypadat tenká vrstva oleje na vodě a chod obou pro nás podstatných paprsků.
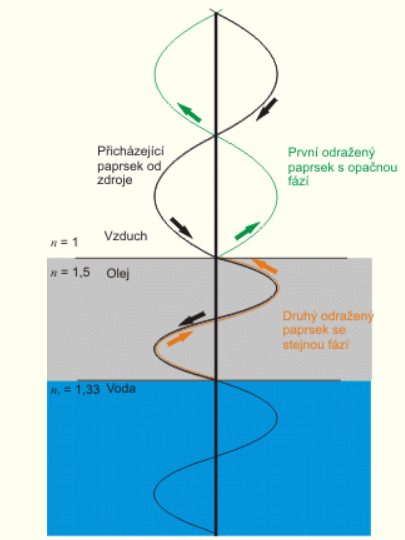
Černý paprsek jde od zdroje a narazí na první rozhraní. Část paprsku se odrazí (v obrázku nakresleno zeleně) a část pokračuje dále ve svém směru. Jedná se o rozhraní vzduch - olej, tedy dochází k odrazu paprsku na opticky hustším prostředí, a proto má zelený paprsek opačnou fázi, což odpovídá dráhovému rozdílu:
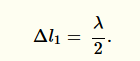
Část černého paprsku, která pokračovala ve směru šíření, dorazila na další rozhraní olej - voda, kde dochází k odrazu na opticky řidším prostředí a dráhový rozdíl odraženého oranžového paprsku je dán jen jeho delší dráhou, tedy:
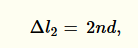
kde n je index lomu materiálu (v tomto případě oleje), d je tloušťka olejové vrstvy. Tloušťku olejové vrstvy násobíme dvěma, protože paprsek musí projít olejem tam a zpátky, takže geometrickou dráhu musíme započítat dvakrát.
Celkový dráhový rozdíl obou paprsků je dán optickou dráhou, kterou musel oranžový paprsek urazit navíc, a tím, že zelený paprsek změnil při odrazu svoji fázi:
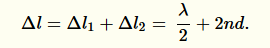
Toto je vztah pro celkový dráhový rozdíl obou odražených paprsků.
Pro maxima platí, že rozdíl optických drah se musí rovnat násobku vlnové délky.
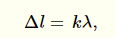
Odpověď:
Po odrazu na olejové skvrně se nejvíce zesílí vlnová délka λ = 400 nm (odpovídá pro k = 2), takže ji uvidíme fialovou.
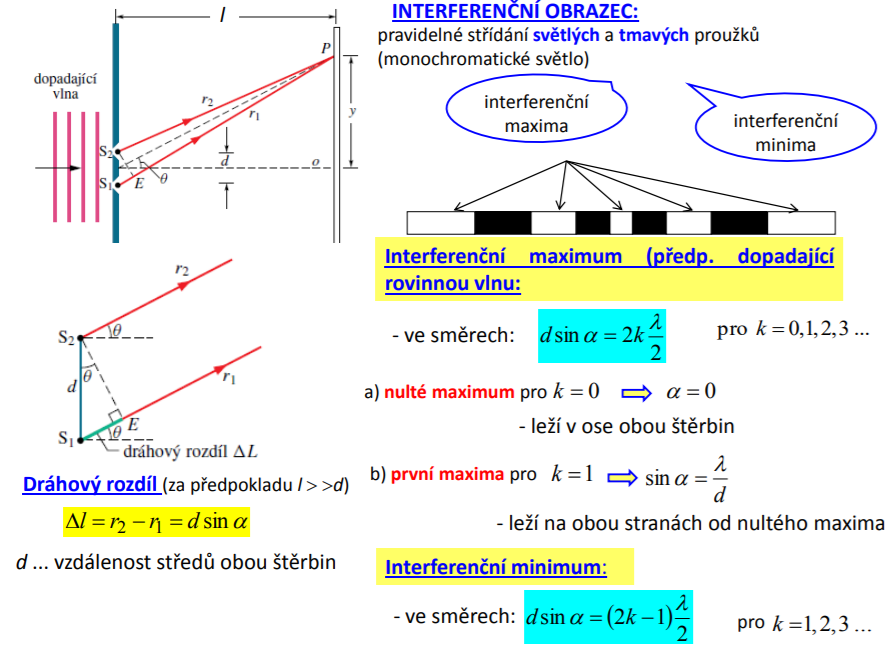
Young - pokus
Kde všude se s interferencí setkáme:



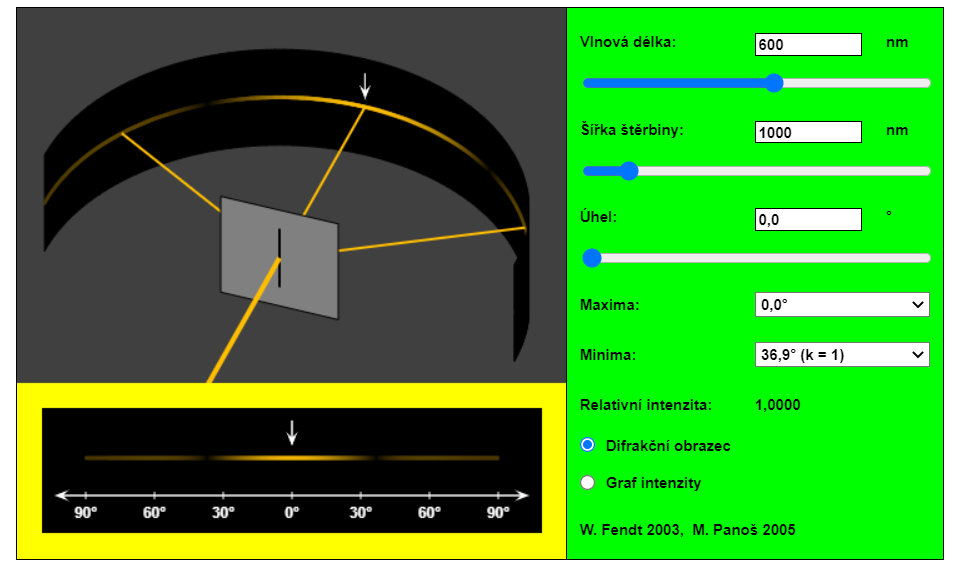
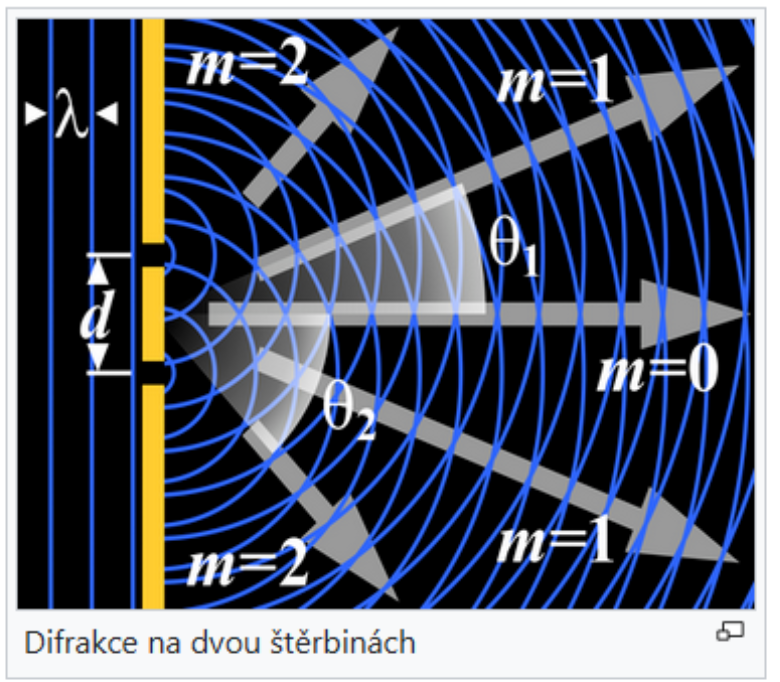
Ohyb světla na štěrbině

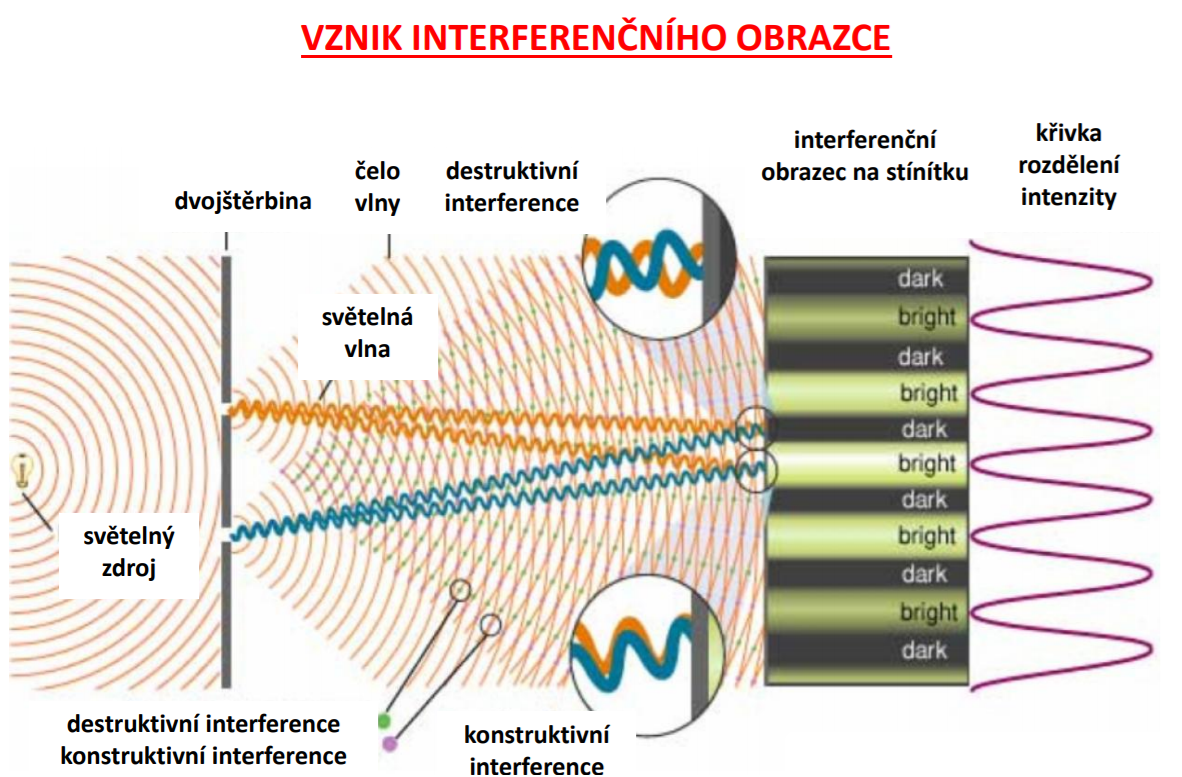
Difrakce světla
Odchýlení světla od přímočarého směru šíření, které není způsobeno odrazem či lomem. Nastává na překážkách, které mají velikost srovnatelnou s vlnovou délkou světla.
Důležitý je průchod světla štěrbinou, která je podle Huygensova principu zdrojem elementárních vln.
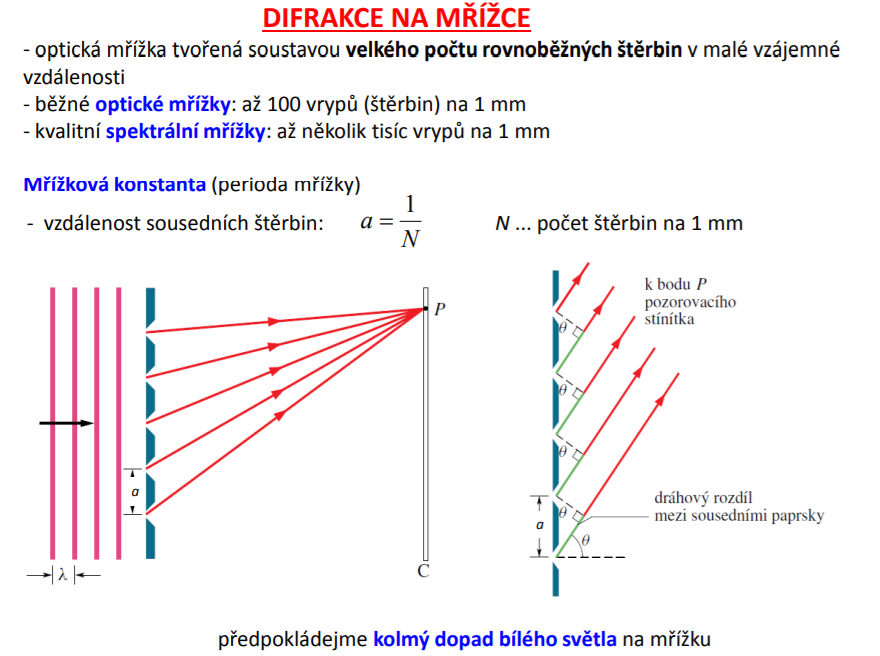
Optická mřížka je tvořena velkým počtem rovnoběžných vrypů na skle (až 1000 na 1 mm). Neporušená místa představují štěrbiny a vrypy mezery mezi těmito štěrbinami.
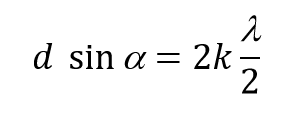
d - mřížková konstanta (vzdálenost štěrbin)
alfa - úhel vycházejících paprsků,
k - řád ohybového maxima
lambda - vlnová délka světla
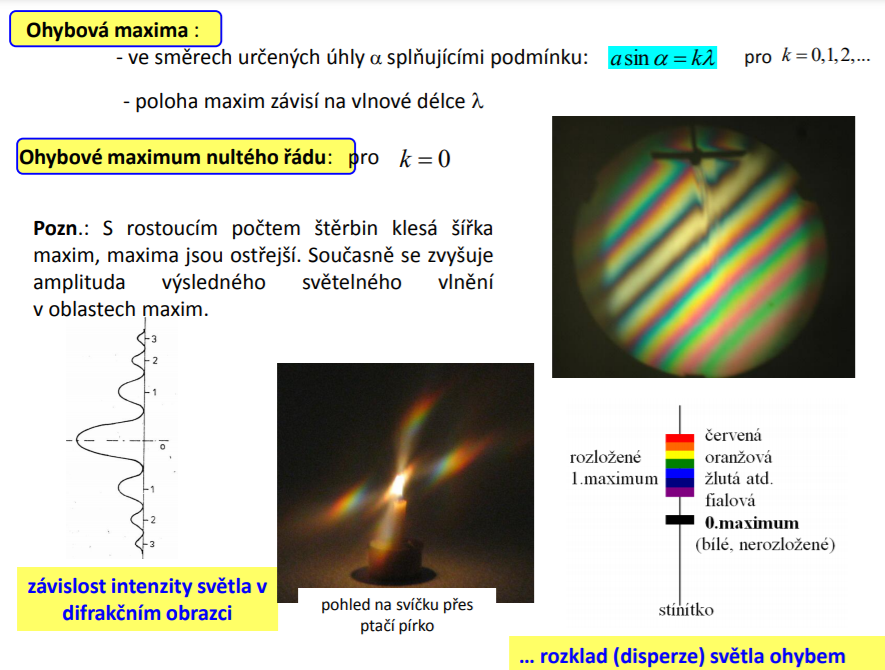
Z rovnice vyplývá, že při průchodu bílého světla vznikne interferencí ohybové mřížkové spektrum, kdy je nejvíce odchýleno červené a nejméně fialové světlo.
Polarizace světla
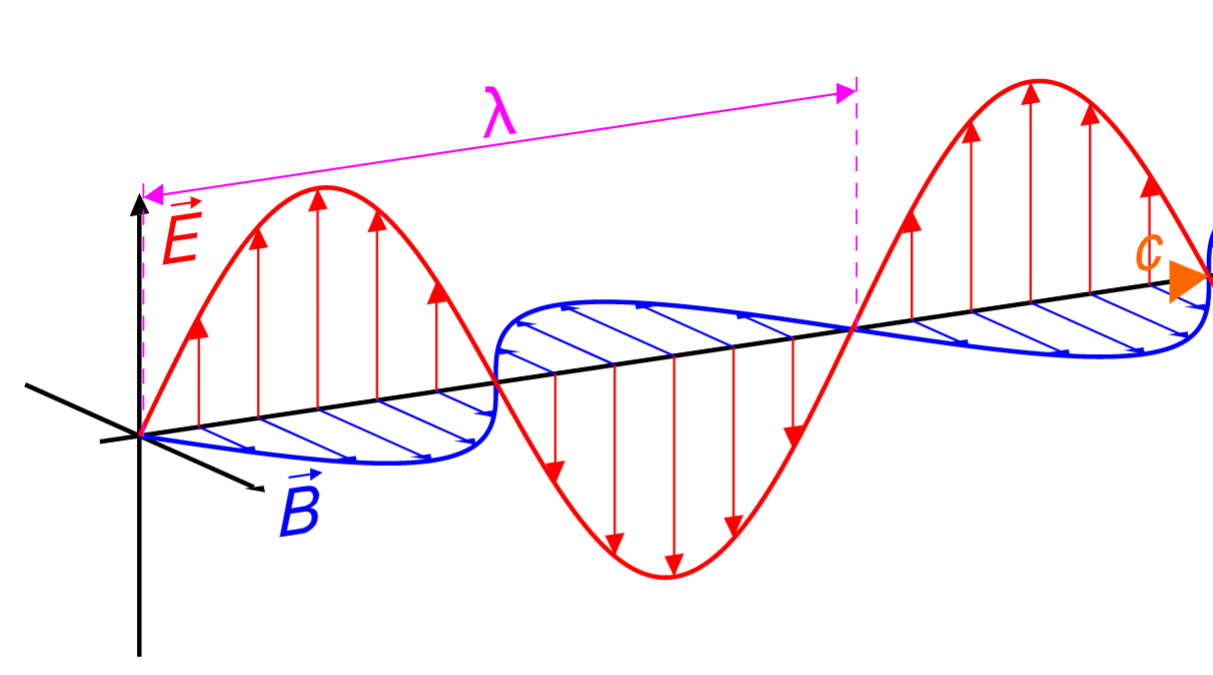
Přirozené světlo je nepolarizované. Jde o příčné elektromagnetické vlnění, charakterizované kmity navzájem kolmých vektorů E a B. Na sítnici oka působí jen kmiání vektrou intenzity el. pole E. V polarizovaném světle probíhá vlnění vektoru E v jedné rovině.
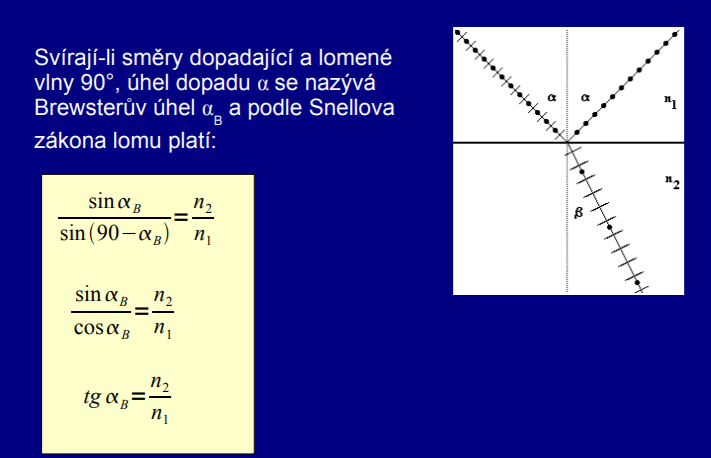
Úplná polarizace nastane, když je úhel dopadu roven tzv. Brewsterovu úhlu. Při tomto úhlu je odražený paprsek kolmý na lomený paprsek.